Disclaimer: I dont claim to completely understand what monads are as I am still learning more about them but this is my attempt to explain it how I understand it. Please correct me (in comments) if I got something wrong
Story time
In my last post I wrote about Railway Oriented Programming (ROP) which was a very elegant way of handling errors, exceptions and chaining functions so that the code is much more understandable and has all the error handling, without all the if & else's. Scott Wlaschin in his talk regarding ROP said that it is just a use case of Monads but with a much better metaphor. Many people also commented about the same thing regarding my previous post, that it's just monads.
Dear railway oriented programming haters: tools != practices. Saying "just use Either with Kleisli composition" is not helpful to noobs 1/3
— Scott Wlaschin (@ScottWlaschin) March 26, 2015I agree with his tweet but after getting ROP I wanted to understand monads as I was amazed by the ROP use case of it and actually understanding ROP made it easier for me to understand monads as I have a concrete example of where it's useful. In my search to understand them better I found a video by Brian Beckman where he does a really good job of explaining different concepts and build it up to explaining what monads are. In this post I am going to follow his pattern and at the end give a concrete example of its usefullnes by reiterating some of the things in my last post.
Function composition
Lets first discuss what functions are and what is function composition. Function is mapping that takes something from one end and spits out something on the other end. No matter how many times you call the function you should always get the same output from it as long as the input remains same. sin(x) is a good example of mathemetical function, the sin(90) will always result in 1.
Lets define a notation for describing this function
// Sin function in Math class in C#
public static double Sin(double a) {...}
// To make it simpler we will define this function as
sin : double -> double
// Here we are saying that sin takes an input of type
// double (tail side of arrow) and has an output of type
// double (head side of arrow). We will use the same
// notation in this post
The basics of functional programming is that we create bigger functions by using smaller functions this allows us to define very complex system in very simple terms as at the lower level everything is a small function that does one thing and does it very well.
Think of it as bricks for your program which you can combine to form a wall and then combine walls to form a building. This is called composition where you combine smaller functions to make bigger functions.
Now lets say we have two functions i.e. f: a -> a and g: a -> a, here a is any type like generics in C#. Lets compose function f and g.
h(a) = f (g (a))
This is simple composition where the output of g(a) becomes input to f and that returns something of type a
The type of h will be
h: a -> a
// In C# the composition will
// look something like this
public static a h<a>(a input) {
return f(g(input));
}
// EOF
This is how we chain or compose functions to make bigger functions. Let say we have magic operator `•` which helps us in composing functions hence `h` can be defined as `h = f•g` which is equivalent to `h(a) = f(g(a))`. So now you have an idea what function composition is and why it is there i.e. to make bigger functions from smaller ones to keep things simple.
Monoids
Function compositions is essence of monoids so you have a way of composing functions of same types to make a more complex function of same type, just as we did with f and g to create h. Lets take Brian's metaphor of a clock to explain monoids.

Monoids are
Collection of things with a rule of combining the things. That rule obeys some other rules.
Lets see what that means in terms of clock. Here the hours are collection of things (lets say we dont care about AM & PM) and the rule of combining the hours is (x+y)%12 where x and y are hours from clock. With this rule we will always get a number which is some hour in the clock. This rule which we can call as clockadd and represent it as º obeys some other rules. These rules are as follows
1- Associativity
xº(yºz) = (xºy)ºz
Lets dissect it (x=3, y=6 and z=10)
xº(yºz)
( 3 + ((6+10)%12) )%12 = 7
(xºy)ºz
( ((3+6)%12) + 10 )%12 = 7
So we can see this obeys associativity.
2- Identity
Here lets assume I is an identity where
xºI = Iºx = x
In case of clockadd the identity I is 12
Lets take x=3
xºI
3º12
(3+12)%12 = 3
Iºx
12º3
(12+3)%12 = 3
Hence we can see numbers in clock with clockadd obeys identity rule
If anything obeys these two rules then its a monoid. For monoid commutative is not a requirement i.e. f(g(a)) is not necessarily equal to g(f(a)) an example will be cos(sin(a)) != sin(cos(a)). So you can see number with + operator is also a monoid where 0 is identity.
Monads
Monads are similar to monoids but with a slight change. In case of monoids we had the following functions
f: a -> a
g: a -> a
h: a -> a (created by composing f and g)
In case of monads we will have following functions
f: a -> Ma
g: a -> Ma
h: a -> Ma
The difference here is that instead of returning something of type a we now return Ma where M is some metadata wrapped around a.
Now the question is how do we combine these functions as the return type of the function is not similar to what other functions take an input.
Lets consider we have a magical operator >>= called bind that helps us do that. Lets define a simple notation to create anonymous functions a.k.a lambdas
\a -> (...)
Above is an anonymous function that takes in a parameter of type a and does something with it inside the brackets.
In C# lambdas are defined as
var func = (a) => {...}
Now how do we compose the f and g functions to create h
\a -> ( g(a) ) >>= \a -> ( f(a) )
Types: a -> Ma >>= a -> Ma
|-----------------------|
Here bind operator >>= takes Ma as input and unwraps the metadata M associated with a and pass it to the next function. In this way we can compose such kind of functions.
So what is the type of >>= bind operator? Its Ma -> (a -> Ma) -> Ma that means it takes a wrapped type of Ma as first parameter and a function whose type is a -> Ma and then returns Ma.
Side effects are inevitable in any program other wise there is no use of a program. By side effect I mean any change of state or getting input from user, updating DB etc. In case of functional programming we want to contain such side effects. Here M can be consider a side effect. With monads you keep all functions in your program pure, by passing in the world (or a relevant subsection thereof) and outputting the calculated value including world modified by side effect. Here the world is that metadata M associated with your value
Monads also follow the same rules as Monoids i.e. Associativity & Indentity.
Practical example
Lets see how monads work in action and then you'll understand them a lot better. I'll reiterate things here from my previous post, if you want to understand more about it then go read that, it will help.
A typical application contains some data and some set of operations performed on it. Usually errors in an imperative language are handled by try catch or checking that the each operation(function) returned as expected and if not then return error. This causes a lot of defensive coding by adding a lot of if into the code hence making it difficult to reason about.
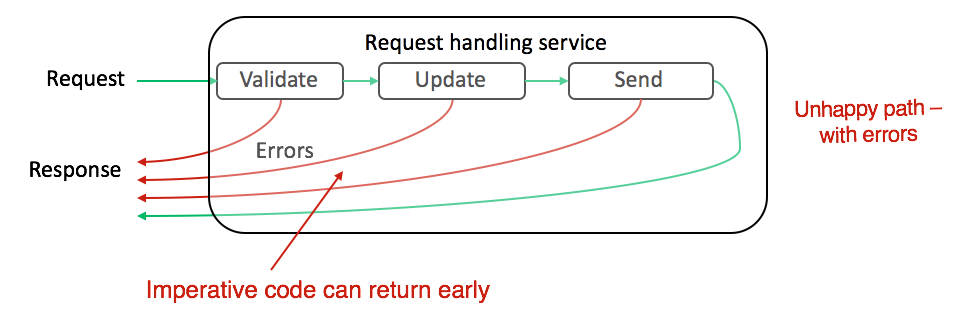
Now lets take how we can handle errors in a functional paradigm in a better way. Lets say that each function returns either {:ok, "data"} in case of success or returns {:error, "Failure reason"} in case of failure. We can call such function two-track functions. Now if we chain such functions then in case of error we dont want to execute rest of the functions but instead bypass them
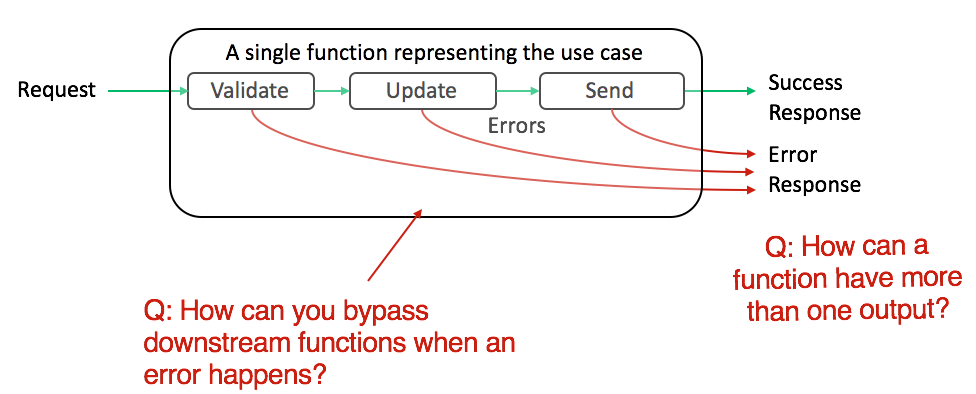
So a railway metaphor works really well here. You have a railway track which you take in case of success and switch the track in case of failure
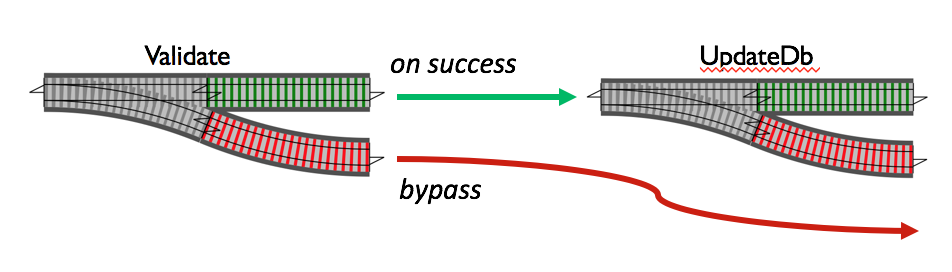
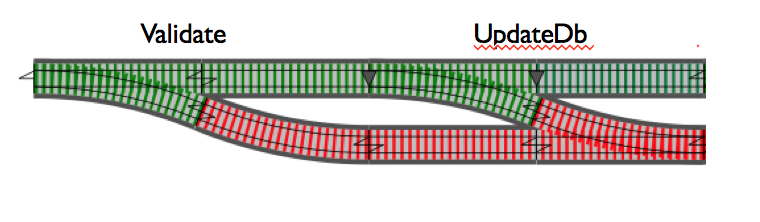
Here {:ok, _} or {:failure, _} is the wrapper M on "data" so Ma here is {:ok, "data"} or {:error, "failure"} so type of a is string.
The operation of joining the two tracks is the bind operation >>= and the rule it joins it with in this case is that it gets input {:ok, _} then call the next function otherwise in case of {:error, _} bypass it. Simple isn't it?
Lets assume we have a request coming in from a user which we need to validate then get user from database, update user in database and send him an email. We have the following functions
- Validate Request: Validates the request values.
- Get User: Gets the user from DB.
- Update DB: Updates the DB
- Send Email: Send email to user.
This example does not conform to syntax of any language and is just a pseudo language (inspired from Elixir)
def validate_request(request) do
if valid request
return {:ok, request}
else
return {:error, "Invalid user id"}
end
def get_user(request) do
if able to get user from DB
return {:ok, user}
else
return {:error, "Issues retreiving from DB"}
end
def update_db(user) do
if able to update DB
return {:ok, user}
else
return {:error, "Unable to update DB"}
end
def send_email(user) do
if able to send email
return {:ok, user}
else
return {:error, "Issue sending email"}
end
As you can see each function is taking an input and returning either {:ok, _} or {:error, _}. So each function has type as follows
validate_request: request -> M request
get_user: request -> M user
update_db: user -> M user
send_email: user -> M user
Now lets see how will we process the request
def create_response({:ok, _}) do: return HTTP_200_REPSONSE
def create_response({:error, _}) do: return HTTP_500_RESPONSE
def process_request(request) do
result =
{:ok, request}
>>= validate_request
>>= get_user
>>= update_user
>>= send_email
return create_response(result)
end

We used the bind operator to join all those functions and in this particular case bind is defined for data type {:ok, _} {:error,_} to pass unwrapped value to next function in case of success otherwise bypass all functions. That is a very practical use of Monad.
Hope this might have demystified a little about what monads are.
Reference
Brian Beckman: Don't fear the Monad
Functors, Applicatives, And Monads In Pictures

